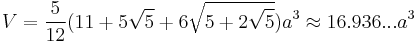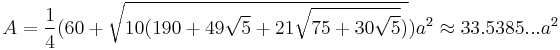Elongated pentagonal gyrocupolarotunda

Elongated pentagonal gyrocupolarotunda

Type	Johnson J₄₀ - J₄₁ - J₄₂
Faces	3.5 triangles 3.5 squares 2+5 pentagons
Edges	70
Vertices	35
Vertex configuration	10(3.4³) 10(3.4².5) 5(3.4.5.4) 2.5(3.5.3.5)
Symmetry group	C_5v
Dual polyhedron	-
Properties	convex
Net

In geometry, the elongated pentagonal gyrocupolarotunda is one of the Johnson solids (J₄₁). As the name suggests, it can be constructed by elongating a pentagonal gyrocupolarotunda (J₃₃) by inserting a decagonal prism between its halves. Rotating either the pentagonal cupola (J₅) or the pentagonal rotunda (J₆) through 36 degrees before inserting the prism yields an elongated pentagonal orthocupolarotunda (J₄₀).

The 92 Johnson solids were named and described by Norman Johnson in 1966.

Formulae

The following formulae for volume and surface area can be used if all faces are regular, with edge length a:^[1]

$V=\frac{5}{12}(11%2B5\sqrt{5}%2B6\sqrt{5%2B2\sqrt{5}})a^3\approx16.936...a^3$

$A=\frac{1}{4}(60%2B\sqrt{10(190%2B49\sqrt{5}%2B21\sqrt{75%2B30\sqrt{5}})})a^2\approx33.5385...a^2$